Al-Karajī: His Contribution On Arithmetic, Algebra, Binomial Theorem and Mathematical Induction

By Akmal Zulkarnain

INTRODUCTION AND BIOGRAPHY OF THE SCHOLAR

Abu Bakr ibn Muhammad ibn al-Husayn al-Karaji (Born 13 April 953 – Died around 1029) was a Persian mathematician and engineer who has made massive contributions to the development of 10th century mathematics, particularly in the field of binomial theorem (Selin, 2008). Al-Karaji was born in Karaj, a city near Tehran (in modern day Iran) but has flourished and written many of his works in Baghdad. Among the works that Al-Karaji has completed (and has been studied by historians of mathematics) are Al-Fakhri fi al-jabr wa al-muqabala, Al-Kafi fi al-hisab, and Al-Badi' fi al-hisab.

Now, the name ‘al-Karaji’ imposes many controversies among historians of mathematics. His name appears (in many old texts and manuscripts) as either al-Karaji or al-Karkhi. This dispute is of a significant importance, for the name ‘al-Karkhi’ means that this mathematician is born in Karh, a suburban area in Baghdad (modern day Iraq) as opposed to Karaj, a city which is in Persia. Rashed (1994) commented that the name al-Karaji is much more plausible, when he examined the arguments in support of the name given by a linguist and historian studying manuscripts on Arabic mathematics, Gorgio Levi Della Vida in 1933. Both Rashed (1994) and Suzuki (2002) are of the opinion that the name ‘al-Karaji’ is more likely to be correct (Rashed, 1994; Suzuki, 2002). For practical purposes, we will refer to this mathematician as al-Karaji from now onwards.

Al-Karaji wrote extensively in mathematics and engineering. His most renowned and studied work is the Al-Fakhri fi al-jabr wa al-muqabala (Glorious on Algebra) which was initially dedicated to the ruler of Baghdad, the place where he devoted his life to study. Later in his life, he gave up on mathematics, and devoted his time writing on engineering in a country he described as the ‘mountain countries’. He died in 1029.

THE CONTRIBUTIONS OF AL-KARAJI IN MATHEMATICS AND ITS APPLICATIONS IN ECONOMICS

PROVED THAT ARITHMETIC ALGORITHMS MAY BE APPLIED ON POLYNOMIALS

One of the first major contribution al-Karaji made to the development of the discipline of mathematics was in his work on algebra in al-Fakhri. Al-Karaji managed to completely free algebra from geometrical operations. Rashed (1994) stressed this out in his work by saying; ‘the more-or-less explicit aim of [al-Karaji's] exposition was to find the means of realising the autonomy and specificity of algebra, so as to be in a position to reject, in particular, the geometric representation of algebraic operations.’ (Rashed, 1994). To fully appreciate and understand this point, we need to venture into the contributions of al-Karaji’s predecessors in the development of algebra, and the context which al-Karaji was writing his work.

Al-Karaji’s work, al-Fakhri fi al-jabr wa al-muqabala, was a commentary on the works of previous Muslim mathematicians on algebra, notably al-Khawarizmi’s al-jabr wa al-muqabala. Al-Khawarizmi (and a few other Muslim mathematicians of his time) developed the discipline of algebra, for the sole purpose of dealing with practical and pragmatic issues faced by the Muslim ummah, particularly in inheritance of land, trade, lawsuits, digging of canals, geometrical computations and others (Rosen, trans, 2010). Because of that, almost every algebraic problem al-Kawarizmi solve in his work needs a geometrical representation. For example, the problem of ‘completing the square’ to find the roots of a quadratic equation (say, x2 + 10x + 39 = 0), was initially solved by al-Khawarizmi using a geometrical representation of the problem;

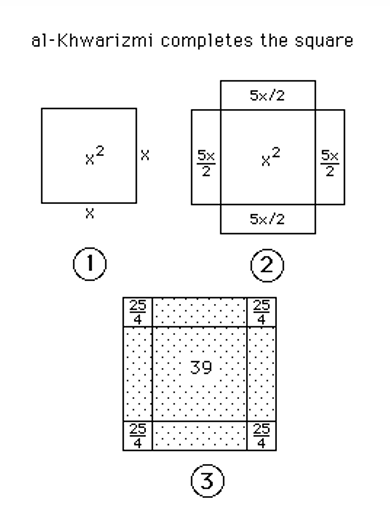
Figure 1: A concise explanation of the figure. Adapted [reprinted] from Al-Khawarizmi (2010) The algebra of Mohammed ben Musa, (Rosen, F. Trans.). Kessinger Publishing LLC, Whitefish, Montana. Copyright 2010 by Kessinger Publishing LLC

The workings of al-Khawarizmi’s ‘completing the square’ method is not of our interest and will not be discussed here, but what is important is that the usage of geometrical representations to solve algebraic problems was, before al-Karaji, the mainstream method. Al-Karaji abandoned geometrical representations and justification for algebraic operations, and employed purely arithmetic operations (subtraction, addition, multiplication and division) on them, in a project named by Suzuki (2002) as the ‘arithmetization of algebra’ (Suzuki, 2002). This is indeed, a new departure in the field of algebra.

Suzuki (2002) remarked that al-Karaji successfully dealt with the algebra of powers higher than two (cube). He gave the following names to the higher degree algebras:

Table 1: Note. Reprinted [adapted] from Suzuki, J. (2002) A History of Mathematics, Prentice Hall, Inc., Upper Saddle River, New Jersey, Unites States. Copyright 2002 by Prentice-Hall, Inc.

In many of his workings, al-Karaji used the abbreviations in the ‘text’ column above to represent the variables in the ‘al-Karaji’ column. Hence, 6x5 + 3x2 + 1/x2, which would be read as ‘six square-cubes plus three squares plus one part-square’ is thereby written as ‘6sc plus 3s plus 1 ps’ (note: in Arabic alphabets) (Suzuki, 2002). Note that during his time, equations and functions are usually written in full text. Here al-Karaji contributes in the early step in the development of modern algebraic notation.

Al-Karaji then noted that these higher degree terms polynomials may be treated exactly like the digits of a multidigit number (Suzuki, 2002). He then proceeded to prove that

3x6 + 2x6 = 5x6, by adding up the coefficients, and doing the same with subtraction of one polynomial with the other, 3x6 – 2x6 = x, by subtracting the coefficients of the polynomials.

And

3x6 × 2x3 = 5x9, by adding up the power of the polynomials, and doing the same with division of one polynomial with the other, 3x6 ÷ 2x3 = 5x3.

Note that, al-Karaji’s work portrays a simple but extremely important conclusion that polynomial expressions could be added, subtracted, multiplied and divided, using the same algorithms applied to operations with numbers, without any reference to geometry.

This has a massive contribution on the field of economics. All thanks to the detachment of algebra from geometry by al-Karaji, economists nowadays would not have to go through the tedious process of finding roots of a quadratic or cubic equation by constructing geometrical representation of the equation. There are a lot of economic applications of quadratic and cubic equations, for example, to find the variable short-run production cost of an automobile company (Pindyck & Rubinfeld, 2015). If one carries out an empirical research by collecting data of the variable costs of the company, upon doing so, one may use either quadratic or cubic equations to represent the shape of the cost curve.

VC = βq + γq2 (quadratic equation to represent a parabolic cost curve)

Or

VC = βq + γq2 δq3 (cubic equation to represent a cubic curve)

Without the contribution of al-Karaji, economists would hassle around the task of constructing geometrical representation of these equations only to find the roots (value of q when cost equals zero) of the equation thus finding the solution(s).

Apart from that, the ‘arithmetization’ of algebra by al-Karaji made possible important and helpful operations with polynomials by economists. Al-Karaji’s contribution in successfully proving that algebraic polynomials may be treated with arithmetic algorithms means that economists may use polynomials in their theorem on production etc. Take the reformulation of Cobb-Douglas production function by Felipe and Adams (2005), for a concise example:

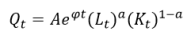
Where,

Qt = (Lt)a(Kt)1-a was the original formulation of the Cobb-Douglas production function

Aeφt is the constant exponential rate of growth of profit and wages

Note that this reformulated Cobb-Douglas production function employs a lot of polynomials into the equation. Without the finding al-Karaji made that polynomials may be treated with arithmetic algorithm as is an integer, this operation in mathematics would not be possible.

THE DEVELOPMENT OF BINOMIAL THEOREM AND THE AL-KARAJI TRIANGLE

Now, the other contribution al-Karaji made is in the development of binomial theorem. Al-Karaji dealt with the problem of expanding binomials that are being raised by an exponent greater than 2. The binomial (a + b)2 is relatively easy to expand (to get a2 + 2ab + b2), but as we go higher up, the work will get more and more tedious, say, for example, to expand the binomial (a + b)6.

Al-Karaji tried to deal with this problem by constructing a structure similar to the famous Pascal’s Triangle – in fact, we may assert that Karaji’s table is a pioneer to the Pascal’s Triangle! – in order to figure out the binomial coefficient as we go higher up the power of a binomial.

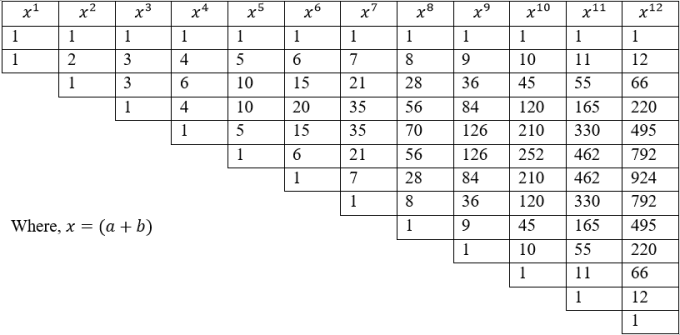
Figure 2: A concise explanation of the figure. Reprinted [adapted] from Berggren, J. L. (2007) Mathematics in Medieval Islam. In Katz, V. (Ed.) The Mathematics of Egypt, Mesopotamia, China, India, and Islam. (pp.515-670). Princeton University Press, New Jersey

The above table is extremely useful in finding the binomial coefficient of higher degree binomials. For example, if one wishes to find the binomial coefficient of (a + b)4, from the table we know that they are 1, 4, 6, 4, and 1. Using this, we may get the entire expanded binomial (with a few extra tricks that will not be explained here) as:

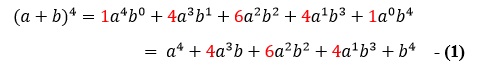
With 1, 4, 6, 4, and 1 as the binomial coefficient of this expanded binomial raised to the power 4. This marks a new development in binomial theorem in mathematics (Berggren, 2007).

Among the application of binomial theorem in economics is the determination of the value of the Euler’s Number , the base of natural logarithm (Ummer, 2012). The Euler’s e = 2.7282 number is used extensively in economics as the proxy for continuous interest compounding, and in growth models, among others (Chiang & Wainwright, 2005). There are a few ways to find the value of the number e, among them, as what may be found in Chiang and Wainwright (2005) is to find the limit of the following equation;

To get e = 2.7182818284590452353602875 …

Or, according to Ummer (2012), economists may use binomial theorem to obtain the value, by using the binomial theorem to expand the equation (1 + 1/n)n, to get

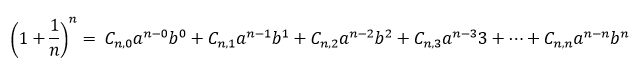
(This is basically the formula we used to obtain (1))

With a few more works that would not be demonstrated here, taking the limit of the above equation as n approaches infinity, we will get the same value of e= 2.7182818284590452353602875 …

ONE OF THE FIRST MATHEMATICIANS TO EMPLOY THE METHOD OF MATHEMATICAL INDUCTION

The last contribution of al-Karaji that will be mentioned in this write-up is that al-Karaji was among the first mathematicians who employed the method of mathematical induction as proof to his theorem, apart from the Greek philosopher Plato (428 B.C.-348 B.C), and the Greek ‘father of geometry, Euclid (Mid-century 4th century B.C. – Mid-century 3rd century B.C.). Using mathematical induction as proof, al-Karaji proved that the sum of the first  natural numbers was 1/2n(n + 1), the sum of the squares of the numbers that follow one another in natural order from one is equal to the sum of these numbers and the product of each of them by its predecessor. Ʃi2 = Ʃi + Ʃi (i – 1) . Apart from that, he also demonstrated that the sum of the cubes of the first  natural number is Ʃi3 = (Ʃi)2 (Rashed, 1994).

Now our interest, in this matter, is not that much on the intricate workings and findings of al-Karaji, but rather on the method he employed to prove the above theorems. Al-Karaji first proved the case for n = 1, then for n = 2, based upon his result in n = 1 . He then carried on proving the case of n = 3 based upon his result in n = 2, and continued until n = 5 (Rashed, 1994). Though this does not count as mathematical induction proper, it is somehow considered as the pioneer effort and one of the first steps towards ‘proof by induction’ in mathematics.

Proof by induction is just one of the many methods of proofs in mathematics. Nevertheless, this method employs a powerful trick that allows us to prove a statement about any arbitrary number, n, by first proving that it is true when n = 1, and then assuming it is true when n = k, and proving that it is true for n = k + 1. In economics, economists use this method is many respect, as a proof for the theoretical models they devise. For example, Seliaman and Duffuaa (2012) used mathematical induction to provide a proof for the theorem they devised for the Generalized Model for the Economic Design of x̄-Control Charts. Control charts are graphs that are used to study how a process changes over time. Seliaman and Duffuaa (2012) studied the theorem that derives the expected total cost and the expected cycle length of a business. They employed mathematical induction as the proof of their theorem stated in the model. This is just one of the many examples of uses of mathematical induction as proofing tools in economics.

CONCLUSION

The contributions of al-Karaji to the world of mathematics in general and economics in particular are both astonishing, inspiring and spectacular. Without his works, mathematics may not be as how it is, and our learning progress in economics may be seriously hampered. May Allah bless al-Karaji’s good soul.

REFERENCES

Adams, G. F., Felipe, J. (2005) “A Theory of Production” The Estimation of the cobb-Douglas Function: A Retrospective View. Eastern Economic Journal, Vol. 31, No. 3, Summer 2005.

Al-Khawarizmi (2010) The algebra of Mohammed ben Musa, (Rosen, F. Trans.). Kessinger Publishing LLC, Whitefish, Montana. (First Edition by Rosen published in 1831, Original work by al-Khawarizmi published in the 8th century).

Berggren, J. L. (2007) Mathematics in Medieval Islam. In Katz, V. (Ed.) The Mathematics of Egypt, Mesopotamia, China, India, and Islam. (pp.515-670). Princeton University Press, New Jersey.

Chiang, C. A., Wainwright, K. (2005) Fundamental Methods of Mathematical Economics. Mc-GrawHill International Edition, New York, United States.

E.K. Ummer (2012) Basic Mathematics for Economics, Business and Finance. Routledge, London.

Pindyck, R. S., Rubinfeld, D. L. (2015) Microeconomics; Eight Edition, Global Edition. Pearson Education Limited, Essex, United Kingdom.

Rashed, R. (1994) The Development of Arabic Mathematics: Between Arithmetic and Algebra, Boston Studies in the Philosophy of Science, Vol.156, Kluwer Academic Publishers, Dordrecht, Netherlands.

Seliaman, M. E., Duffuaa, S. O. (2012) The Principle of Mathematical Induction Applied to the Generalized Model for the Economic Design of x -Control Charts, Open Journal for Applied Sciences, vol. 2, pp. 236-240. Retrieved 27th April 2017 via http://file.scirp.org/pdf/OJAppS20120400005_54610110.pdf

Selin, H. (2008). Encyclopedia of the history of science, technology, and medicine in non-western cultures. Berlin, New York: Springer. p. 131.

Suzuki, J. (2002) A History of Mathematics, Prentice Hall, Inc., Upper Saddle River, New Jersey, Unites States.